こんにちは、やみとも(@yamitomo_blog)です。
この記事では、主に自分のディープラーニング基礎知識の復習のために、現時点で僕の知っている知識をまとめていきます。間違いなどあればコメントで教えていただけると幸いです。
※ コードは主にPyTorchで書いていこうと思います。
ディープラーニングを大まかに分類する
ディープラーニングは僕の観測する範囲では以下のように分類されると思います。
それぞれかなり発展していて内容盛りだくさんなので、まずは自分の興味のある分野に絞って掘り下げて勉強すると良いと思います。
画像を扱うディープラーニング
例えば0〜9までの数字が書かれた画像を入力してどの数字か当てる、など。
Keywords: MNIST, CNN
時系列データを扱うディープラーニング
例えば10日分の株価を入力して以降の株価を予測する。
ある商品のレビュー(文章データ)を入力して良い評価のレビューなのか悪い評価のレビューなのか判定する、など。
Keywords: RNN, 自然言語処理(NLP)
何かを生成するディープラーニング
実在する人の顔の画像をたくさん入力して学習し、存在しない人の顔の画像を生成する、など
Keywords: GAN
ディープラーニングの大まかな流れ
- ディープラーニングフレームワークを使ってモデルを実装する
- モデルに訓練データを与えてモデルを訓練(学習)する
- 性能を評価する
- 訓練済みのモデルを使って課題を解決する
(1) ディープラーニングフレームワークを使ってモデルを実装する
※ ディープラーニングフレームワークとはTensorFlow(Keras)やPyTorchなどのことです。
ディープラーニングフレームワークについては下の記事で少し解説しています。

(2) モデルに訓練データを与えてモデルを訓練(学習)する
モデルの複雑さ、入力するデータの個数、学習の進み具合などを鑑みて適切な回数エポック(epoch)を回します。
1エポックとは、基本的に訓練用に用意したデータ全てを1周することです。
学習は数エポックで十分だったり、難しい課題だったりすると100エポック以上回す必要があります。
回すエポック数はハイパーパラメータです。(ハイパーパラメータとは最終的に人の手で調整する必要のあるパラメータ)
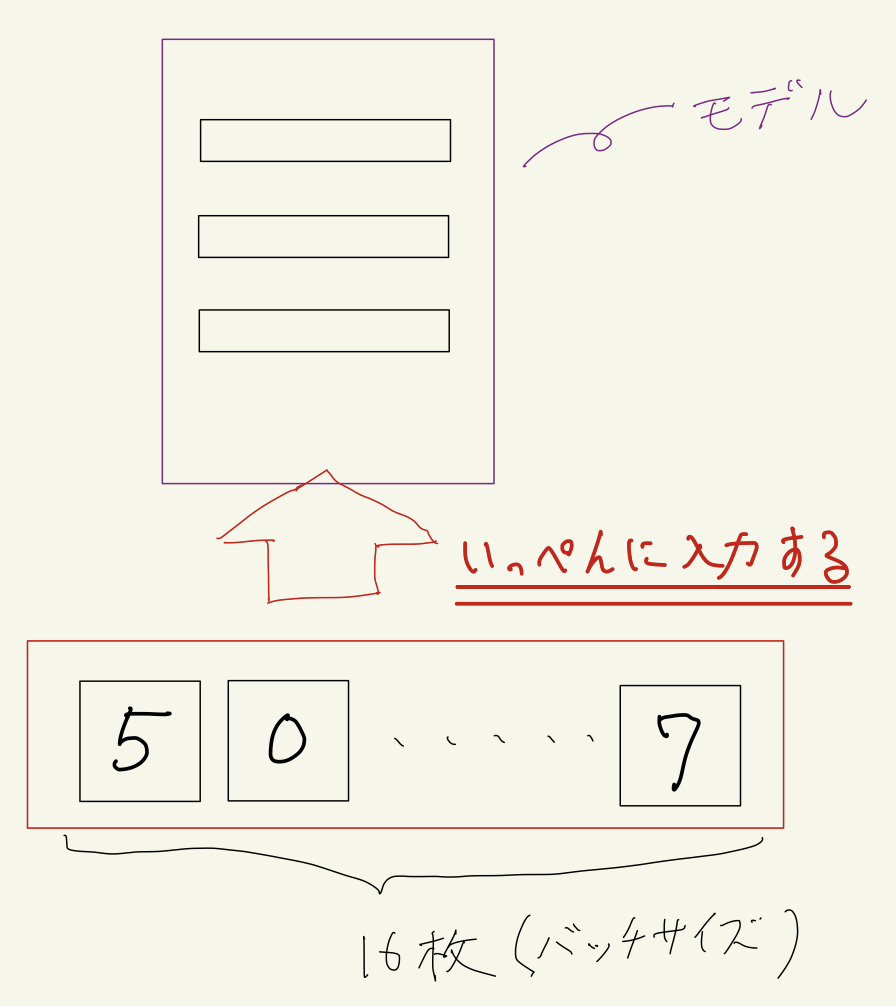
データは基本的にバッチ(batch)という単位でモデルに入力します。
例えば、0〜9の画像を入力して数値を当てるディープラーニングモデルに対して、0〜9のどれかが書かれた画像を1枚ずつ入力するのではなく、例えば16枚ずついっぺんに入力します。
この16枚1セットをバッチと呼び、1バッチに何個データを含ませるか(この例では16という数字)をバッチサイズと呼び、これもハイパーパラメータとなります。
バッチサイズは16、32、64、128、256、512などの2の冪の数字が使われることが多いです。
画像を入力する場合などは特にバッチサイズが大きいとGPUのメモリに乗らない(GPUメモリが足りない)場合があるので、その場合はバッチサイズを小さくするとうまく動く場合があります。
ただバッチサイズはGPUメモリが許す限り大きくする方が学習が速い気がします。
ただその場合に性能がどうなるかは検証できていないので、自分で色々試してみてください。
モデルの訓練の詳細については、この記事の下の方でさらに詳しく解説します。
(3) 性能を評価する
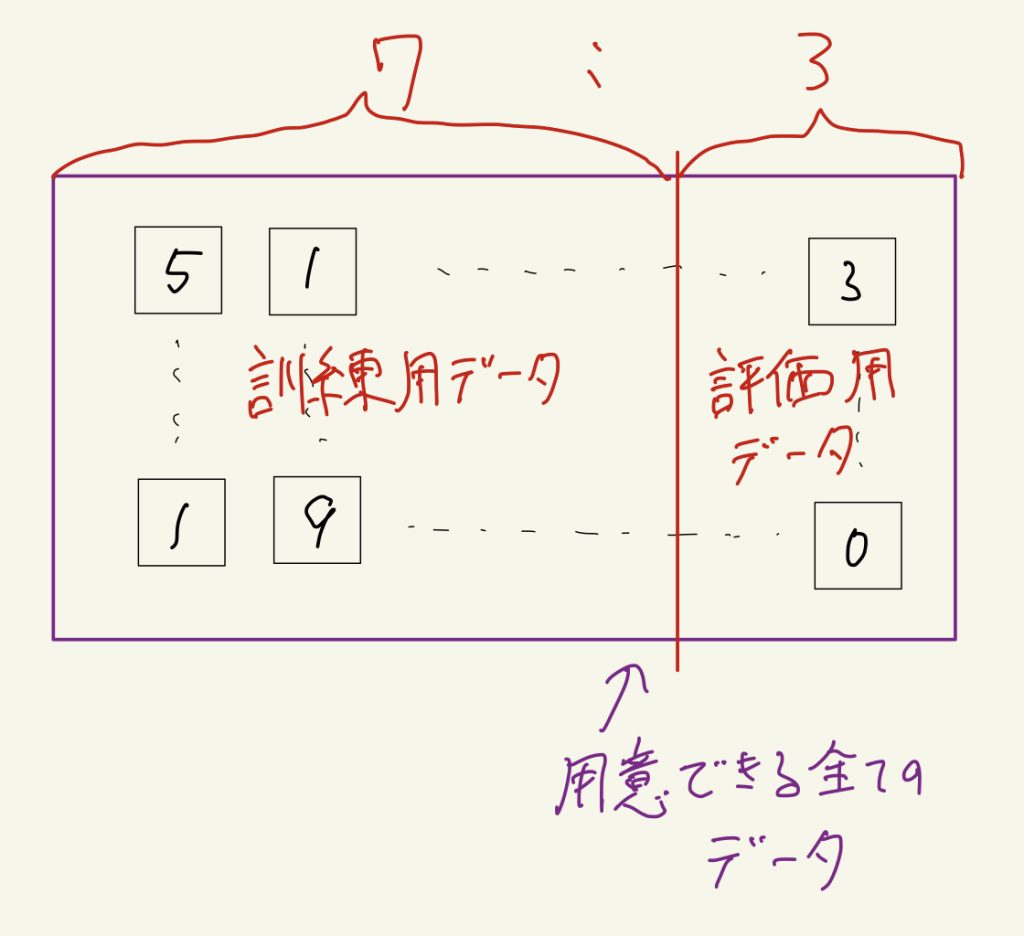
モデルの訓練(学習)に使ったデータとは別のデータを使って、モデルの性能を評価する必要があります。
なので後出しになりましたが、最初の段階で手持ちの全てのデータを訓練用と評価用に分けておく必要があります。
比率としては全てのデータを7:3もしくは8:2の比率で訓練用と評価用に分けると良いと思います。
注意として、モデルの評価を訓練データで行ってはいけません。
なぜならモデルは訓練データで学習したので、訓練データの答えは知っているからです。
ディープラーニングモデルはまだ答えの知っていない新しいデータに対して良い性能を示す必要があります。
(4) 訓練済みのモデルを使って課題を解決する
性能を評価して満足できる正解率などを出せるモデルが訓練できたら、そのモデルを使って本来自分が解決したいと思っていた課題を解決します。
ディープラーニングモデルの訓練の詳細
まず、PyTorchなどのディープラーニングフレームワークで実装されるディープラーニングモデルは基本的に決まった処理を行う層(レイヤー)を重ねたものです。
入力データは最初にテンソルと呼ばれる数値の多次元配列に変換されます。
そしてこのテンソルが入力側の層から順番に流れていき、それぞれの層で層の種類に応じた処理が行われテンソルが変換されていきます。
※ 基本的にテンソルの形状を変える層が多いです
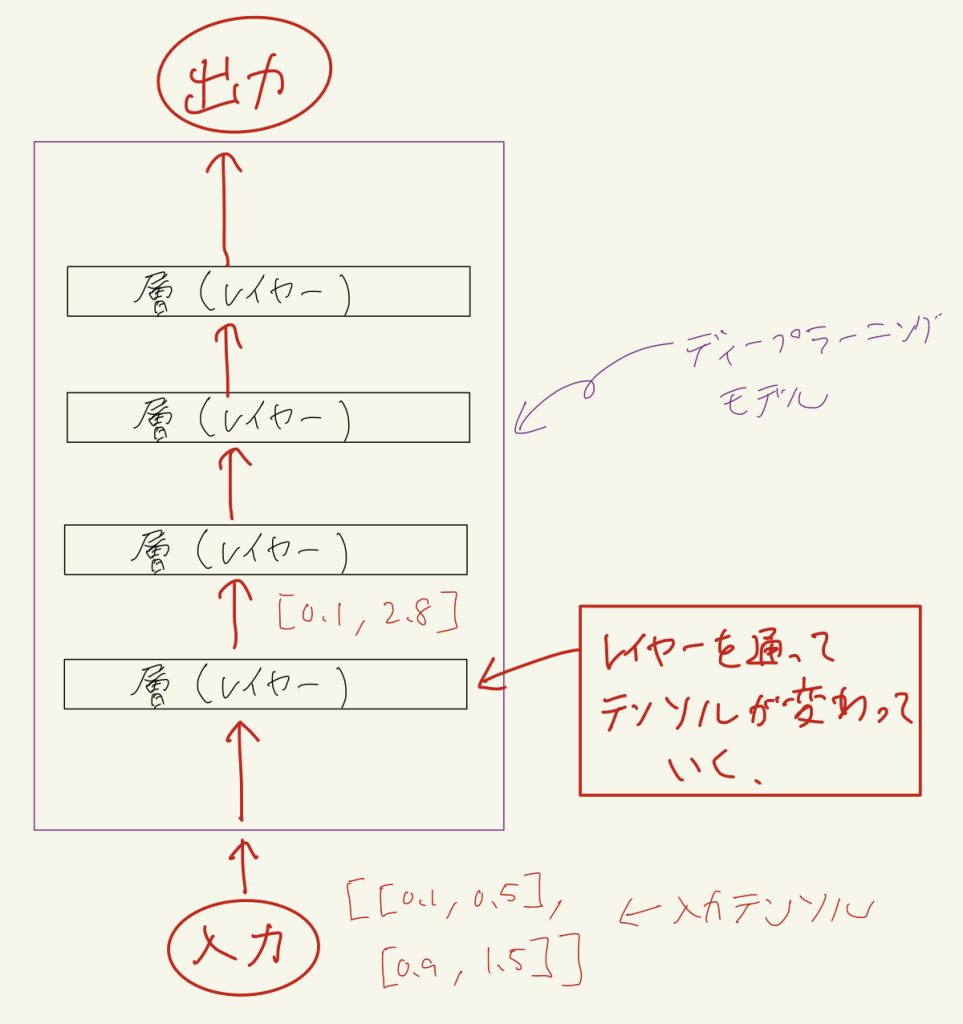
そしてモデルの出力側の最後の層を通って出てきたテンソルがモデルの出力となります。
損失関数(1)
ここで損失関数というものが登場します。
損失関数は「モデルの出力」と「正解ラベル」から「損失」という1つの数値(5.434みたいな)を計算する関数です。
「正解ラベル」とはモデルに入力したデータ1つ1つに対応する正解のことです。
例えば5という数字の書かれた画像を入力した場合、正解ラベルは5となります。
ここまで教師あり学習としてのディープラーニングを説明してきたので、全てのデータには正解ラベルが付いていると仮定します。
損失関数の出す値、つまり損失ですが、この値は大きいほどモデルの学習が進んでいないことを表します。モデルの学習を進めて、この損失の値を小さくしていくことが目標です。
主な層(レイヤー)の紹介
全結合層(Dense, Linear)
PyTorchではtorch.nn.Linearクラス、TensorFlowではtf.keras.layers.Denseクラスが対応します。
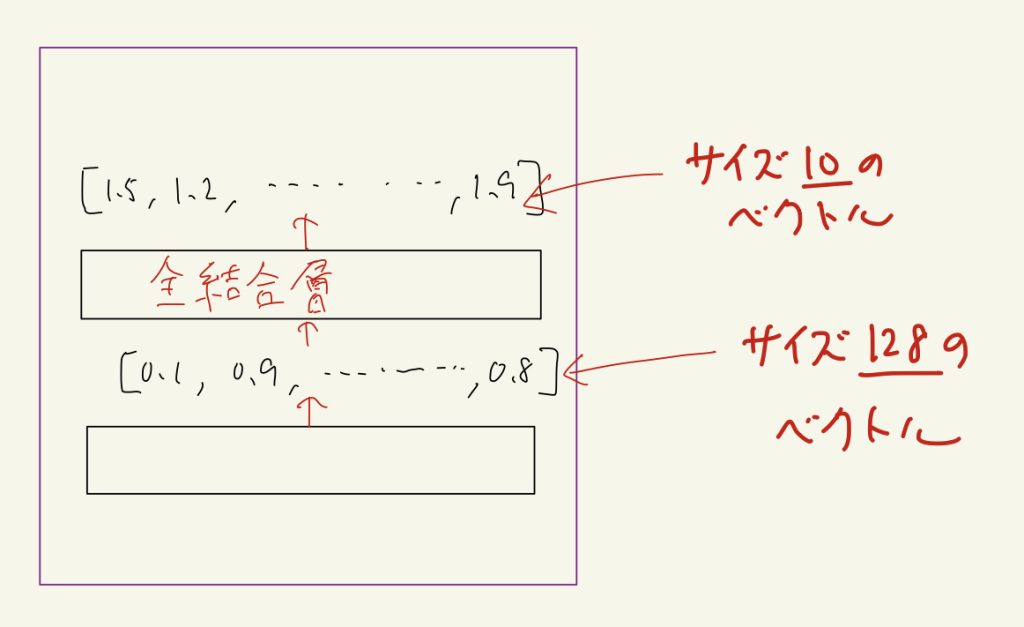
入力をx、出力をyとすると以下のような計算をします。
y = xA + b
Aはこの全結合層が持つパラメータの行列です。bはバイアスと呼ばれるyと同じサイズのベクトルで、このベクトルの個々の値も全結合層のパラメータとなります。
ただし、バイアスbの加算は全結合層を定義する際に無効にすることも可能です。
全結合層の本質的な役割は僕も良くわかっていませんが、僕は単純に出力されるベクトルのサイズを望みのサイズに変える目的で使っています。
例えば全結合層の前の層の出力がサイズ128のベクトルだとしましょう。0〜9の数字を当てるのが目的の場合、最終層の出力はサイズ10のベクトルだと都合が良いです。(数字が10個だから)
このような場合、入力サイズ128、出力サイズ10の全結合層を通せば、出力はサイズ10のベクトルになります。
実際は全結合層の出力に対してさらにソフトマックス層を通して確率に変換したりします。
このように全結合層はベクトルのサイズ変換に便利です。
ソフトマックス(Softmax)層
ソフトマックス層は基本的にディープラーニングモデルの最終層に来ることが多い。
(Attention技術などで最終層以外で用いることもある)
ソフトマックス層は前の層の出力を指定した次元で総和1の確率に変換する。
簡単に実験するコードを示す。
import torch
input = torch.tensor(
[[1, 2, 3],
[-1, 1, -2]]
, dtype=torch.float)
print(input)
softmax_layer = torch.nn.Softmax(dim=1)
output = softmax_layer(input)
print(output)
""" 出力
tensor([[ 1., 2., 3.],
[-1., 1., -2.]])
tensor([[0.0900, 0.2447, 0.6652],
[0.1142, 0.8438, 0.0420]])
"""上のコードの例で説明すると出力の計算式は下のようになる。

指数関数(exp)を使うのは入力の値にマイナスの値が含まれていても都合よく計算するためです。
指数関数(exp)を通すとマイナスも含めた全ての実数が0より大きい実数に変換されます。しかも大きさが保存されたまま。(1 < 2 をそれぞれexpに通してもexp(1) < exp(2)、 -10 < 3をそれぞれexpに通してもexp(-10) < exp(3)、このように大小関係が保存される。)
またソフトマックス層の出力の値はどれも0〜1の実数になることも重要です。だから確率としての要件を満たす。
損失関数(2)
損失関数はタスクごとに適切な関数を選んだり、作ったりする必要があります。
(基本的な損失関数はディープラーニングフレームワークに用意されている)
ここでは「交差エントロピー誤差(cross entropy error)」という損失関数について具体的に説明します。
先ほど説明した「全結合層」「ソフトマックス層」を使った下のようなディープラーニングモデルを想定します。
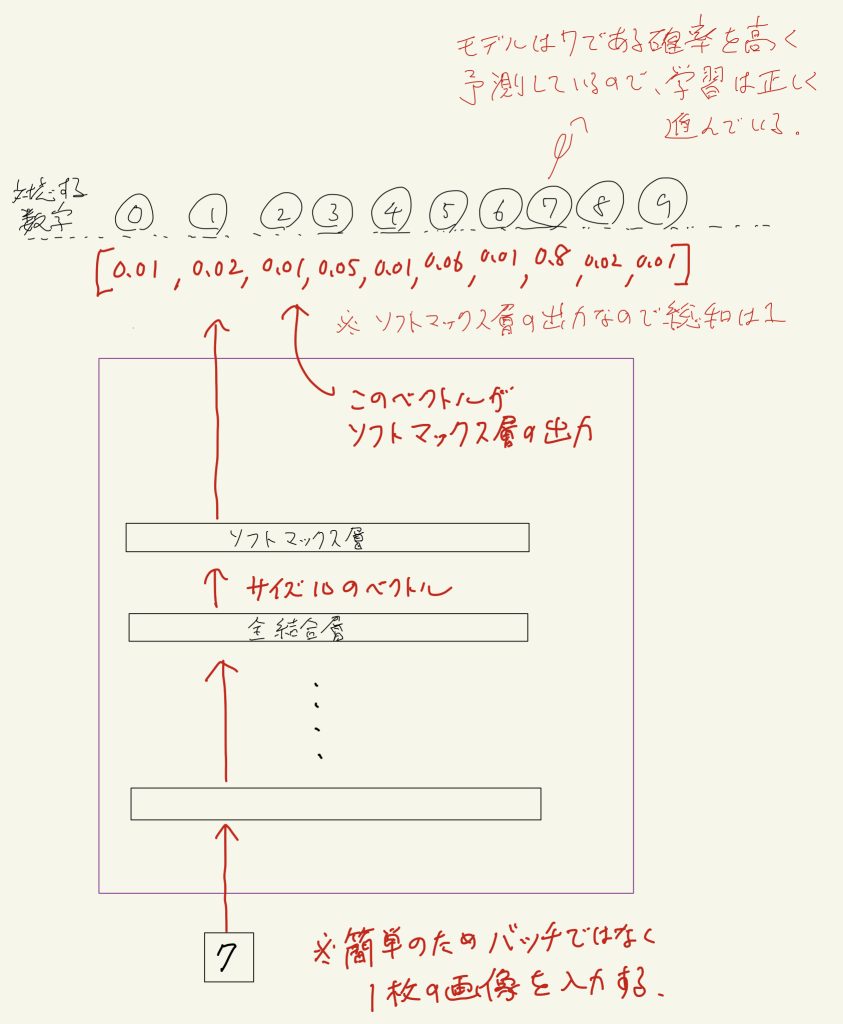
このモデルは0〜9の数字の画像を入力して、どの数字が入力されたのか当てるディープラーニングモデルです。
大体このような10種類から1つの正解を選び出すようなタスクの場合、モデルの最終層で出力サイズ10の全結合層からソフトマックス層で確率に変換します。
例えば、「飛行機」か「鳥」か「牛丼」の三種類の画像を入力し、その3種類のどれかを当てるようなタスクだった場合は、最終層が出力サイズ3の全結合層からソフトマックス層のモデルを構成します。
損失関数の説明に戻ります。損失関数の入力は「モデルの出力」と「正解ラベル」でした。
正解ラベルは大体の場合、下のようなone-hotベクトルです。

one-hotベクトルとは正解に対応する要素だけ1で、他は0のベクトルです。
交差エントロピー誤差損失関数の説明に戻ります。
交差エントロピー誤差関数を超簡単に説明すると、下のようにone-hotベクトルの1に対応するモデル出力の確率にlogを通した値にマイナスを掛けた値です。
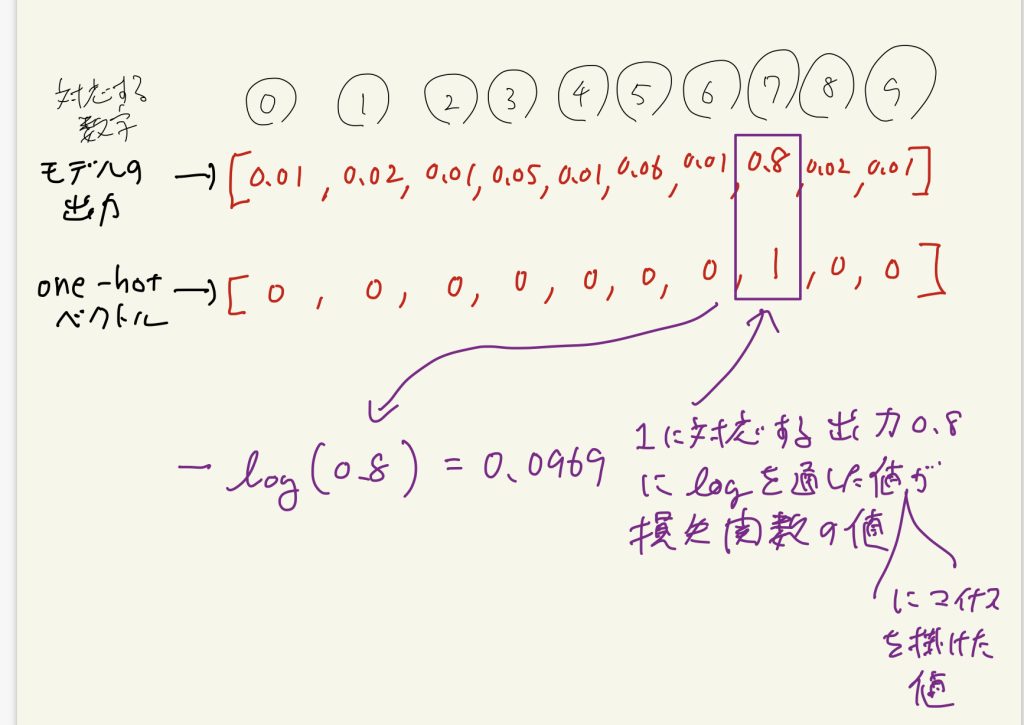
自然対数のlogのグラフを思い出してもらいたいのですが、正解に対応する出力の確率の値を高く予測すればするほど-log(確率)で計算される損失関数の値は小さくなります。
交差エントロピー誤差関数の数式はシグマを使った複雑な式が書かれていることがありますが、やっていることは上で説明したことと同じです。
一旦力尽きたので、今日はここまでにします。明日以降最近やっているRNN周りのことを書いていきます。


