Attentionの論文 ※リンク先のPDFリンクをクリック
※この論文ではAttentionという言葉は用いられていない
attentionの意味は「注意」で、ディープラーニングの文脈でAttentionと言った場合、「注意機構」と呼ばれるモデルの一部に組み込まれた一種の計算構造を表す。
注意機構には、シンプルな注意機構(この記事ではシンプル注意機構と呼ぶ)と、クエリ(Q)、キー(K)、バリュー(V)を使った注意機構(この記事ではQKV注意機構と呼ぶ)、およびいくつかの亜種がある。
この記事ではシンプル注意機構を解説する。
シンプル注意機構
まず登場人物を紹介する。それぞれの呼称は解説のために便宜的に付けたもので一般の呼称ではない。
対象ベクトル・・・「注意」を向ける対象のベクトル。一般に複数ある。
関心ベクトル・・・今現在(その時点)での関心を表すベクトル。どのような情報を欲しているかがベクトルに埋め込まれている。これは、その時点(タイムステップ)で1つ生成される。
上の2つについて補足説明をすると(ここの説明は流してもらっても構わない)、「対象ベクトル」は例えば翻訳タスクで原文側の単語列をLSTMなどのRNNに入力した場合に、各タイムステップで出力される隠れ状態ベクトルだと思えば良い。
関心ベクトルは、同じく翻訳タスクで考えるとデコーダー側で翻訳文を1単語ずつ出力する場合に、それぞれのタイムステップで生成されるベクトルだ。
シンプル注意機構の計算手順
まず、1つ1つの対象ベクトルに対して、その対象ベクトルにどれだけ注意するかを表す「注意スコア」を、1つ1つの対象ベクトルと関心ベクトルを比較することによって生成する。
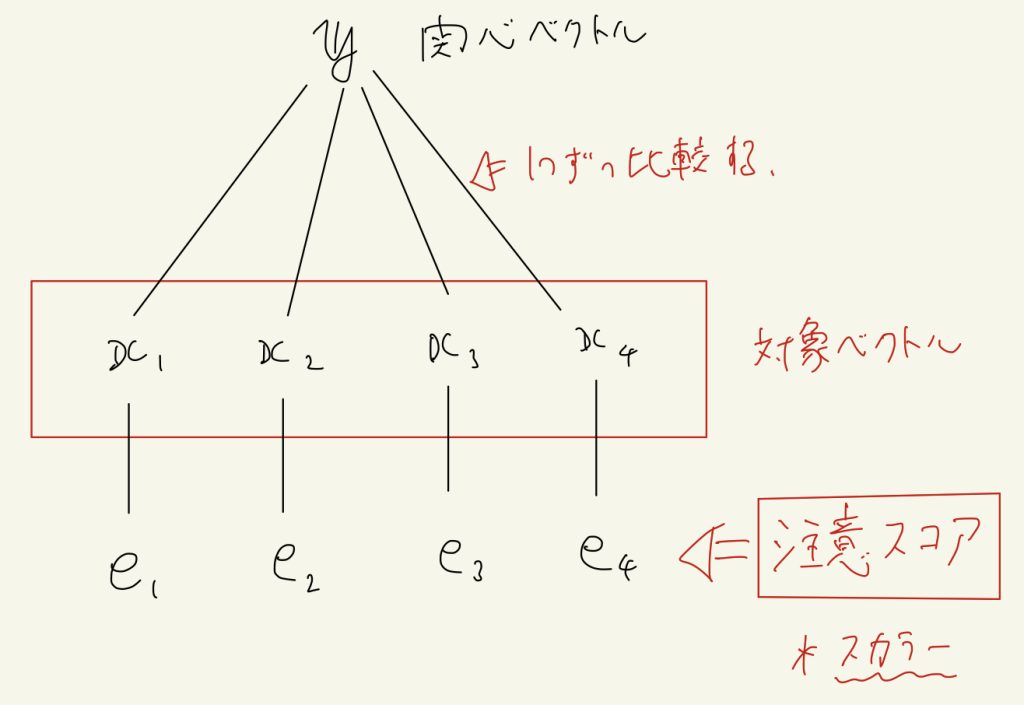
Attentionにいくつか亜種があると言ったのは、この関心ベクトルと対象ベクトルを比較して注意スコアを計算する方法にいくつか種類があるからだ。
この記事では最もシンプルな方法である内積で計算する。つまり関心ベクトルと対象ベクトルは同次元だと仮定し、注意スコアの計算方法は単純に内積で計算するとする。(例:\( e_1 = \boldsymbol{y} \cdot \boldsymbol{x}_1 \))
ここまでで対象ベクトルと同じ個数の注意スコア(スカラー)が計算されている。
この注意スコアについて深掘りすると、例えば現在の関心ベクトルに対して、ある対象ベクトルが非常にどうでも良かった(関心がほとんどなかった)場合、注意スコアはマイナスの値になりうる。
それだと今後の計算で都合が悪いので、ソフトマックス関数を使って、この注意スコアを全て正の値に変換し、総和を1にする。
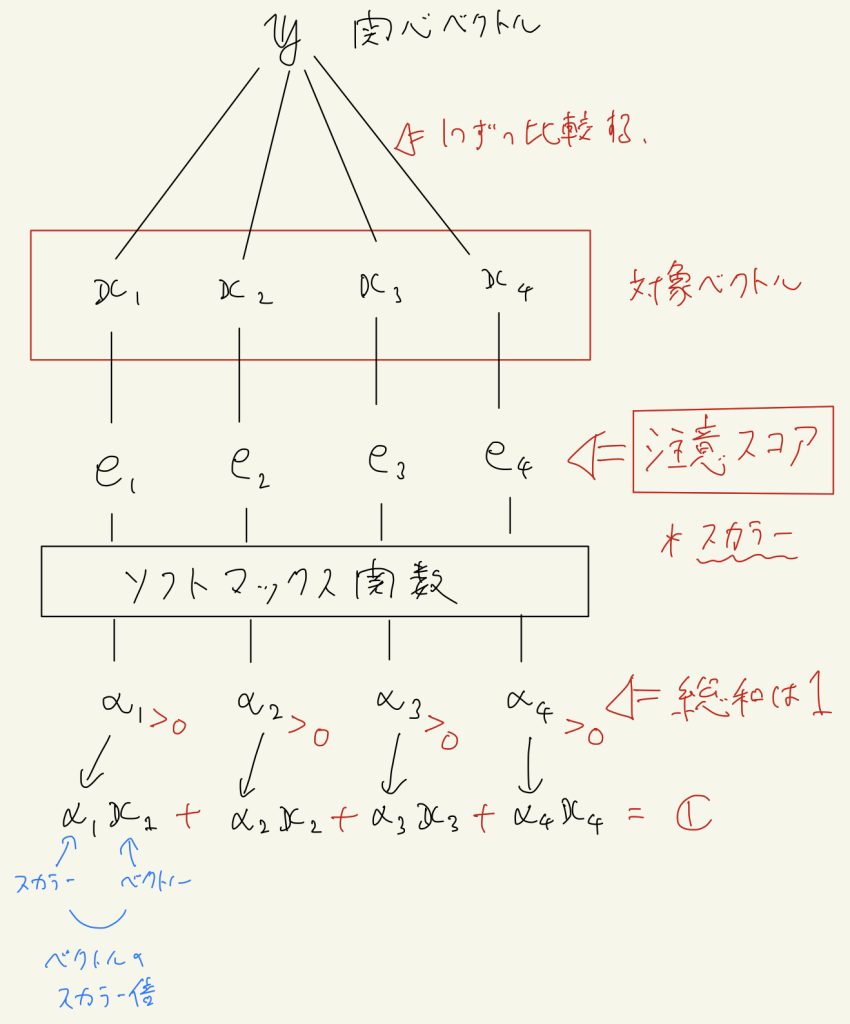
そして対象ベクトルに、対応する注意スコアをソフトマックスで正規化した値\( \alpha_i \)を掛けて(ベクトルのスカラー倍)、最後にそれら全てを足して結果ベクトル\( \boldsymbol{c} \)を計算します。
この最後の計算は、ソフトマックス後の注意スコアを確率とみて平均を取る(期待値を計算する)操作に似ています。
そして計算された結果ベクトル\( \boldsymbol{c} \)は、大きな注意スコアを持っていた(注意の大きかった)対象ベクトルの情報を多く含んだベクトルになります。
この結果ベクトル\( \boldsymbol{c} \)をどう使うかは用途によりますが、このように注意スコアを計算して対象ベクトルの平均をとるのが、おおよそ注意機構に相当する計算だと思っています。
-4

コメント